Maze runner was built while I was completing my artificial intelligence course at uni. I was looking for a project to work on and I wanted to try my hand at implementing some of the search algorithms that I was learning about.

Maze Generation

Mazes are generated using a Depth First Search which searches a branch to its full depth before backtracking to explore other options. By starting with a full grid and removing walls as the search algorithm moves from cell to cell, it is guaranteed that any two cells in the maze are connected by a single path and there are no cycles.

Maze Saving

Mazes are saved to a plaintext file where the first line contains the dimensions of the maze on the first line in the format columns rows. Since the cells are arranged in a rectangular grid, each cell only has bottom and right walls to remove the need to render duplicated cell walls. Each following line is then 2 binary digits representing a cell and encoding which walls are present, bottom right. Therefore, each maze must have columns*rows + 1 lines. Some examples of valid maze files can be seen here.

Maze Solving

There are currently seven solvers supported. These algorithms are all very well documented online, so I won’t go into any real detail about them here, however, the algorithms featured in maze runner include:

These solver’s don’t have any information about where the goal is.

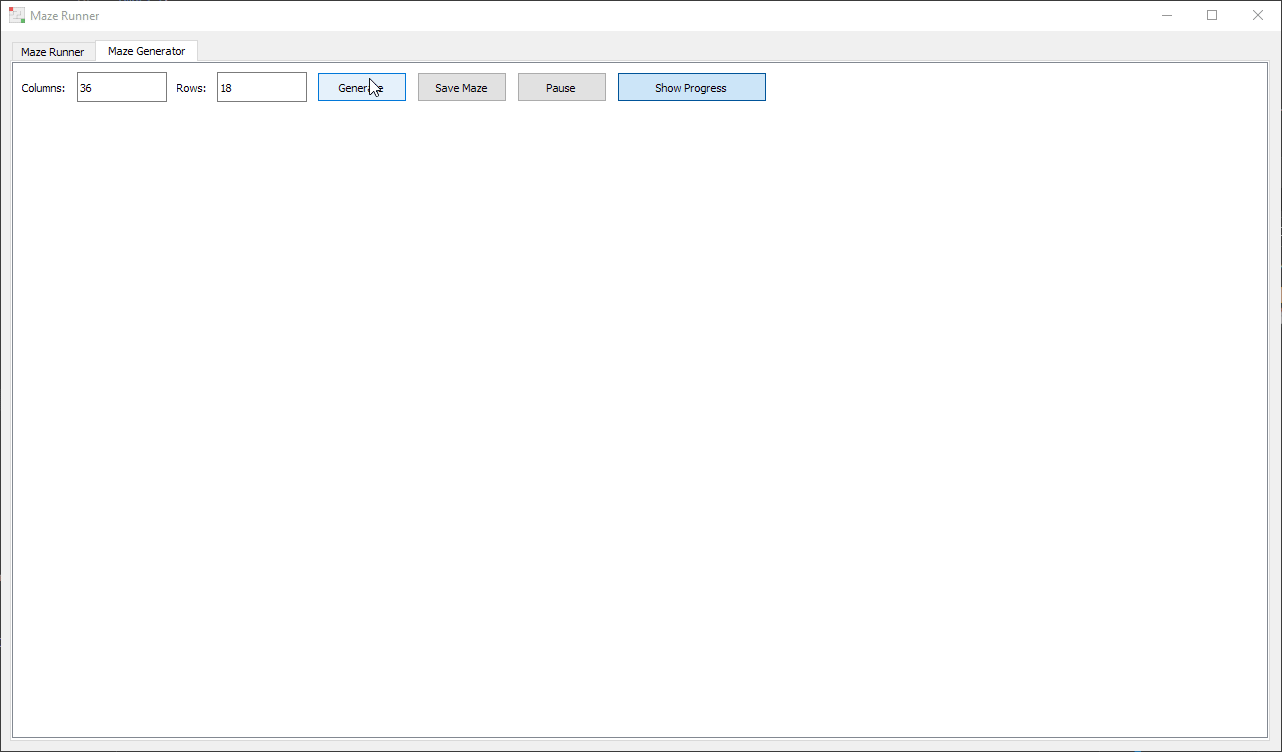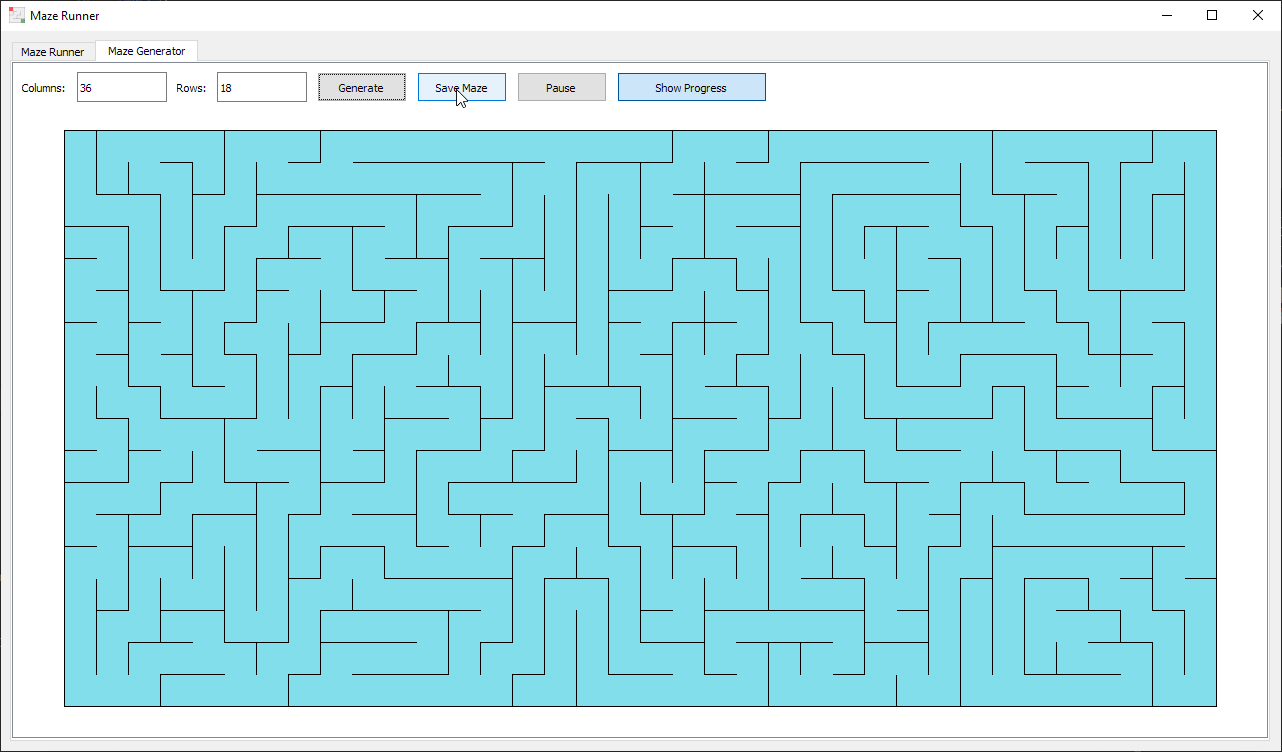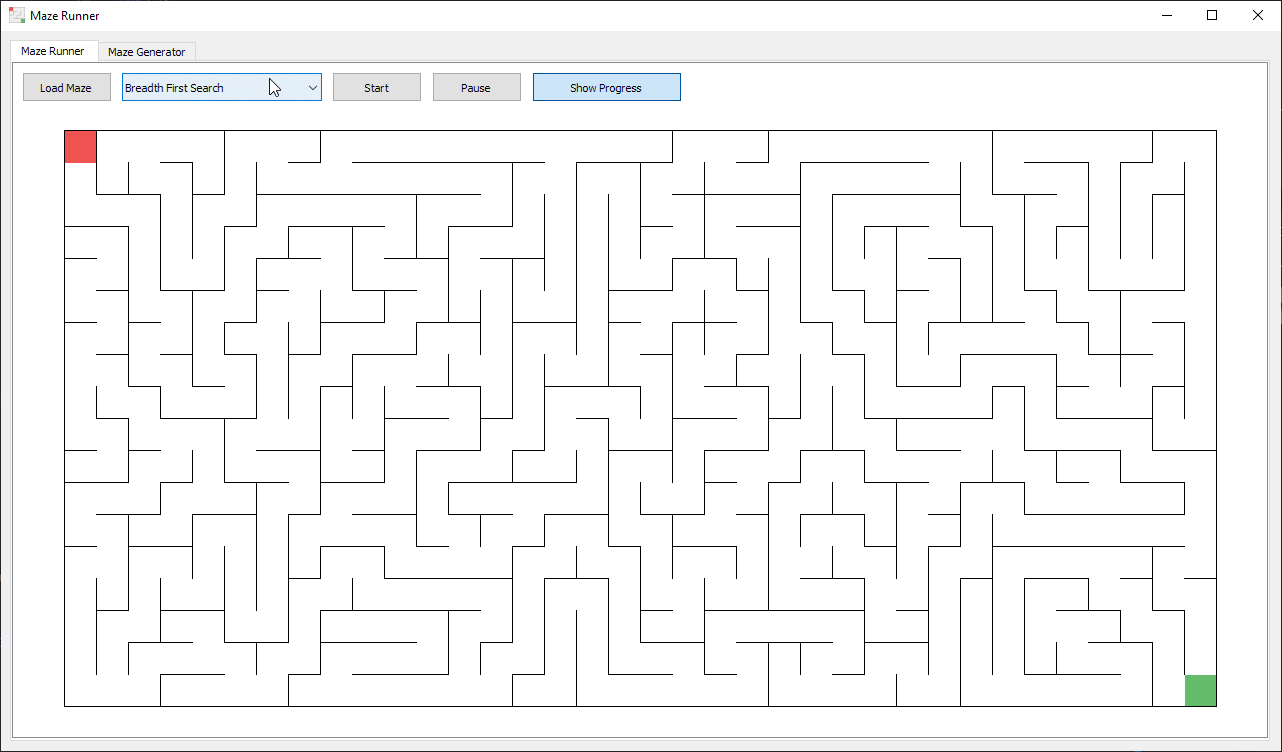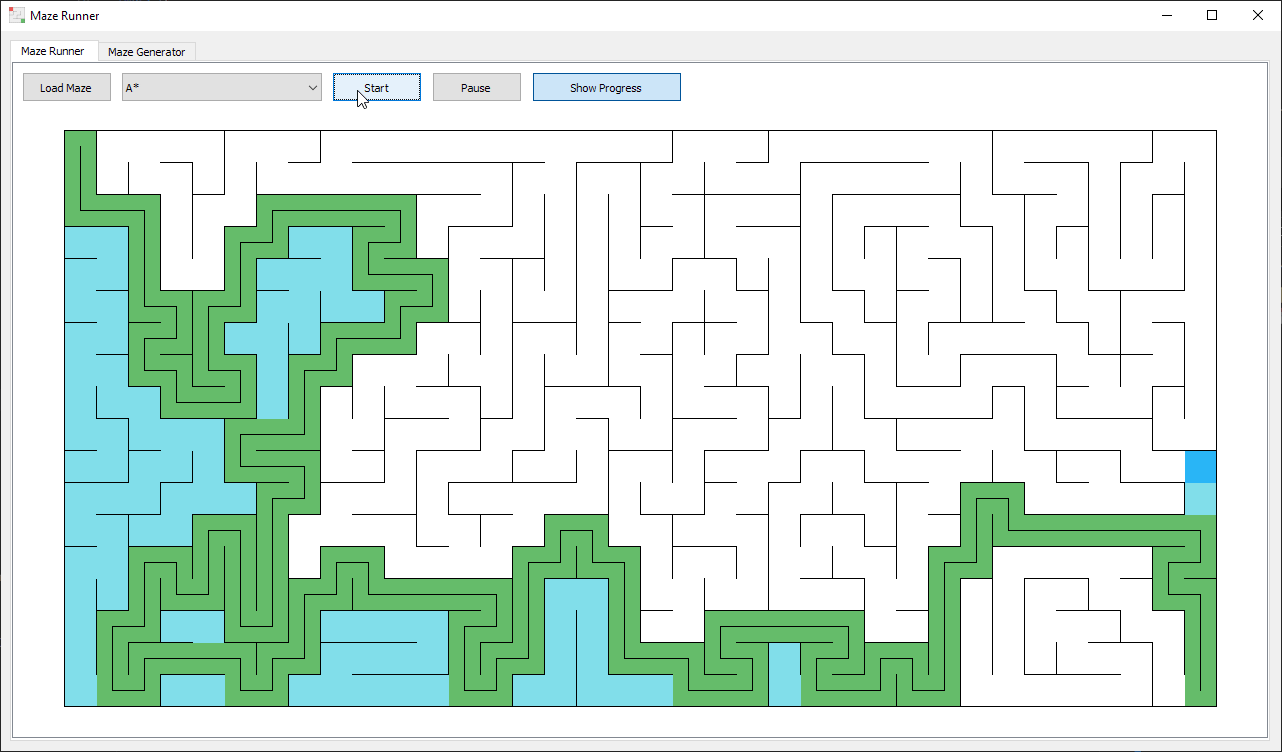
Breadth First Search (BFS)

Maze Runner - Breadth First Search

Breadth first search will explore all cells at a given depth before moving on to cells which are further away. This means all branches are explored equally and is done by adding cells to a queue as they’re discovered.

Depth First Search (DFS)

Maze Runner - Depth First Search

Depth first search operates similarly to BFS except uses a stack instead of a queue. This means that the latest added cell is visited first and thus will continue down one branch until it ends before backtracking to check elsewhere.

Maze Runner - Random Sample Search

A random sample search is performed by randomly placing many points on the search space (this number is configurable in util/Config.py) and using these points to construct a graph. Maze runner constructs and adjacency matrix, linking each point with all other reachable points within a certain distance. A point is considered reachable if a straight line path between the two points does not intersect a cell wall. This graph is then searched using Dijkstra's algorithm to find the shortest path between the start and end cells.

Maze Runner - Bi Directional Breadth First Search

These searches operate the same way as the uninformed searches above except that they start from both the start and end cells.

It includes both bi-directional BFS and DFS.

Informed Seach

Informed searches have information about how far away the goal is which allows them to make more intelligent decisions about the path that they take.

Maze Runner - Greedy Best First Search

Greedy best first search is true to its name, always choosing to visit the neighbouring cell which is the closest to the goal. The distance used to compare is the manhattan distance from the cell to the goal.

Maze Runner - A* Search

A* operates similarly to greedy, except it also takes into account the distance travelled to reach a cell.

Possible Improvements

  • It is currently the case that updating the display is far more intensive than running the search algorithms. It would be nice to add multithreading so that they operate independently.
  • Add the ability to control the speed at which the algorithm progresses.
  • Add other search spaces, and search algorithms for them, such as continous 2D or 3D.
  • Provide statistics about memory usage, cells visited, operations completed etc.