Disco Zoo was a popular mobile game developed by NimbleBit (the creators of Tiny Tower), in which you solve puzzles to rescue animals and expand your virtual zoo. There are 12 regions each with 7 different animals and while the puzzles are interesting to begin with, they don’t really change as the game progresses and so I started to wonder if I could write some code to efficiently solve the puzzles.

The Problem

The game board is a 5x5 grid of tiles hiding 1-3 animals behind them. The player is allowed to uncover a set number of tiles and if all of an animal’s tiles are uncovered, it is rescued and given residence in the zoo. Each animal has a set pattern and so you must use the uncovered spaces and their contents to deduce where the animals will be.

The Solution

First, the board is defined as an array of cells where the top left cell is (0 0). The pattern of tiles that are occupied by an animal is stored as an array of offsets from the top left corner of its bounding box. In the above example, animal 1 would have a pattern of (1 2), (2 2), (2 3) and (3 3). This pattern can then be combined with its location to specify the tiles occupied by a candidate. For example, the candidate for animal 2 would have a position of (2 1) (4 1) and (3 2).

For each animal selected in a game, the solver first generates a set of all possible candidates by ensuring that its bounding box would fit within the game board. For example, the pattern of animal 1 has a width of 3 and a height of 2. Thus there exists a candidate in each \(\text{cell } c_{x, y} \in \{c_{x, y} | 0 \leq x \leq 2, 0 \leq y \leq 3\}\).

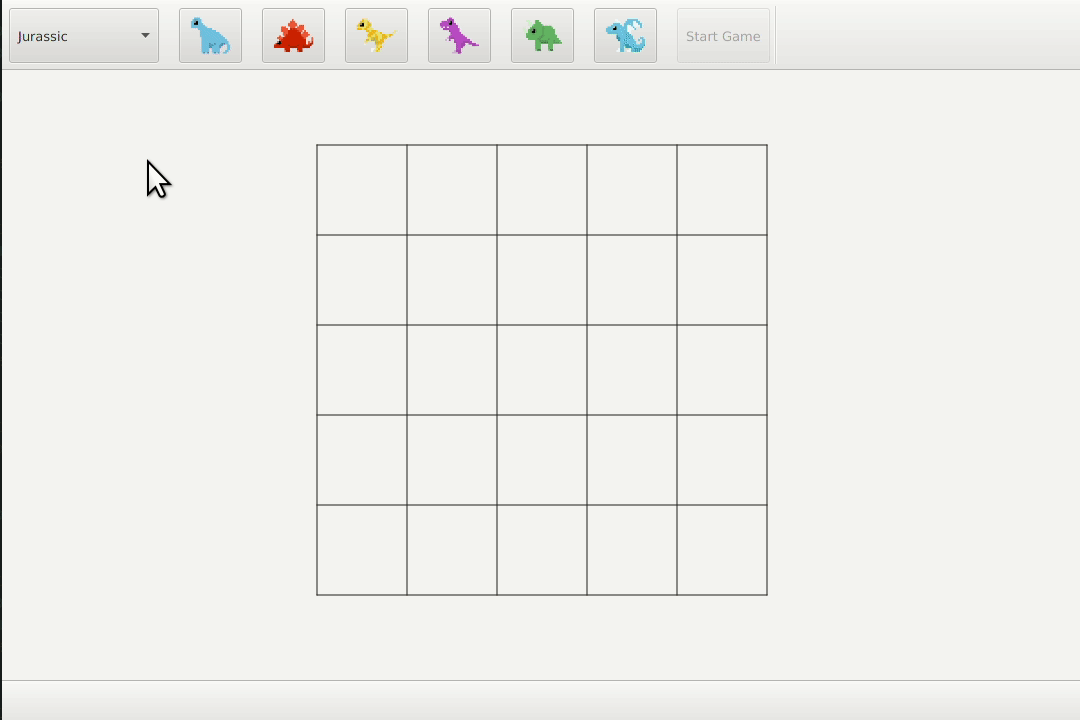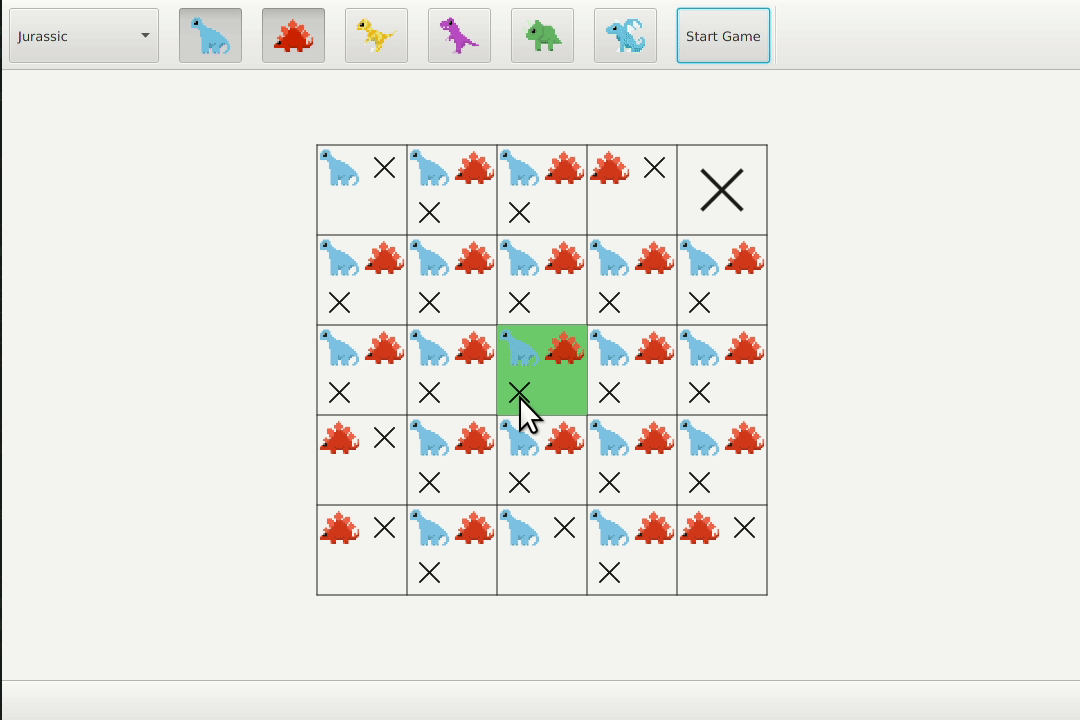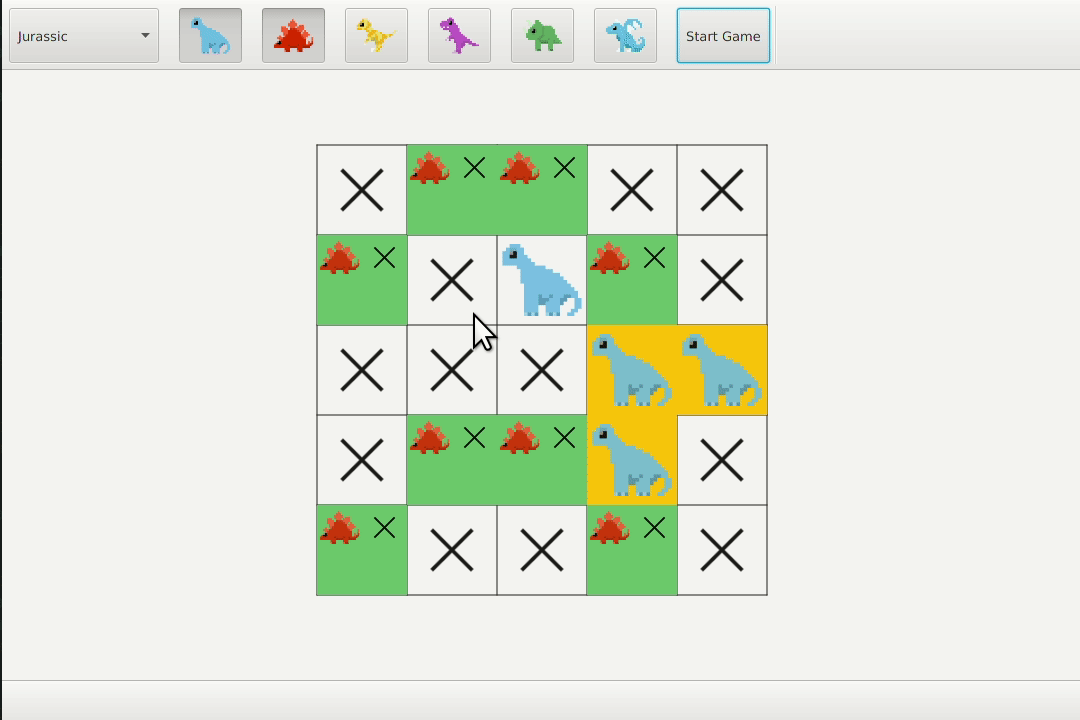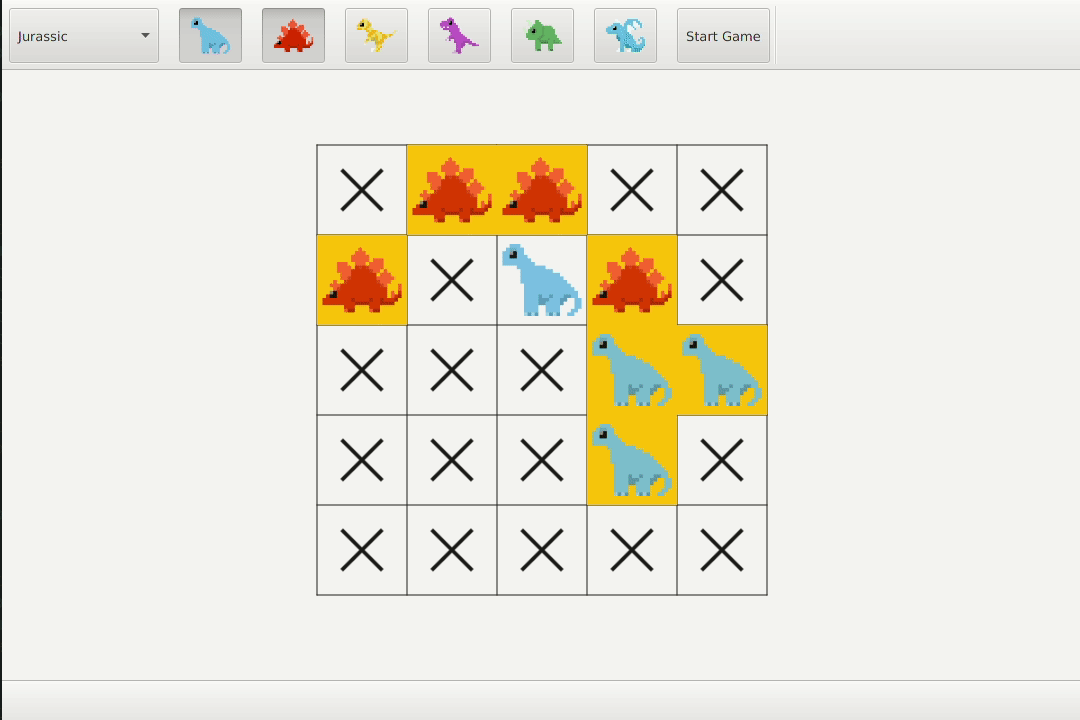
The solver operates by maintaining this set of possible candidates while changes are made to the board and using them to recommend cells most likely to contain an animal (highlighted green) and keep track of cells which are known to contain an animal (highlighted gold).

When the user inputs the contents of a cell, the solver is able to finalise it and there are then three conditions that it checks for.

Occupied cell

If the contents of a cell are known to be empty, then no animal’s candidates can occupy that cell. Similarly, if a cell is known to contain an animal, then no other animal’s candidate can occupy that cell.

If cell (2 1) is known to contain animal 2, then the two shown candidates for animal 1 are not possible.

Known cell

If a cell is occupied by all possible candidates for an animal, then that cell must be occupied by that animal.

If animal 2 only had three remaining candidates and they all contained cell (2 3), then that cell must contain animal 2.

Known candidate

If there is only one remaining candidate for an animal, then it must occupy those tiles.

Animal 1 only has one candidate, therefore cells (1 2) (2 2) (2 3) and (3 3) are known to contain animal 1. It is then the case that animal 2 only has one candidate and must contain cells (2 0) (4 0) and (3 1).

Note: Using this solver does suck the fun out of the game pretty much immediately.

Possible Improvements

The application as it stands offers an incredibly high success rate in maximising rescues however there are several features which could be added to improve the user experience:

• Add an undo button.
• Catch impossible game states and user input errors and reject them rather than just erroring out.
• Allow the user to prioritise the rescue of one animal over any others.
• Provide metrics on the likelihood of each animal being rescued given the number of turns remaining and the board state.